オタク日記
(Mac と Linux, 2016Q3)
目次
2016-09-17 (Sat): Jupyter Notebook (その 2)2016-09-10 (Sat): Jupyter (iPython Notebook)
2016-08-20 (Sat): 宅外サーバのメンテナンス
2016-08-13 (Sat): FreeFem++ と 4 探針法 (その 2)
2016-07-09 (Sat): MathJax 再訪
2016-07-02 (Sat): FreeFem++ と 4 探針法
古い日記:
2016Q2
2016Q1
2015Q4
2015Q3
2015Q2
2015Q1
2014Q4
2014Q3
2014Q2
2014Q1
2013Q4
2013Q3
2013Q2
2013Q1
2012 年
2011 年
2010 年
2009 年
2008 年
2007 年
2006 年
2005 年
2004 年
2003 年
2002 年
2001 年
2016-09-10 (Sat): Jupyter Notebook (その 2)
どうでもいいような titbits …… Jupyter が一語で "iPyothon Notebook" に対応するのではなく、Jupyter Notebook とするのがより正確なようだ。 もうひとつ、Jupiter と発音が同じ (/ˈdʒuːpɪtə(r)/) だと思っていたが、正確には /ˈdʒuːpaɪtə(r)/ らしい。ドキュメントは混乱の極み
iPython Notebook はなかなか動かないと散々文句を垂れてきたが、 そのうちの何割かは (インストールはできているのに) ドキュメントが古いか間違っているせいで最初から躓き、 「使えねぇ」としてしまったような気がする。 とても複雑なシステムが急速に発展しているのだから、 ドキュメントを適切に維持するのは難しいだろう、という事はよく解るが、 それにしても……。まあ、一々ここで論うのは控えておくが、例えば Jupyter Notebook の純正 Help メニューの [Notebook Help] → " Notebook Basics " でさえ、起動するにはipython notebookとしろ、と書いてある……まあ、それでも動くんだけどね :-)
Guido さんによる Python の チュートリアル "The Python Tutorial" みたいに、 「いつも最新」「インストールから起動までカバー」「程良い詳しさ」 「直感的な説明」を兼ね備えたチュートリアルが、Jupyter にもあれば良いのだが……
残念ながらそういうものは見付からないようだが、インストールはともかく、 使い方については、結局は 本家のドキュメントを見るのが最も近道だったかな、と。
しかぁし、ややこしい事に、この http://jupyter-notebook.readthedocs.io の他に、 http://jupyter.readthedocs.io にも一連のドキュメントがあって、 どうもこちらの方が新しいようなのだが、 まだよく「熟れ」ていない——つまり、私には理解し辛い。 このあたりも、「混乱の極み」という印象を持ってしまう一因かも。
インストール補遺
PyVenv で PyPI から pip-tools を使ってインストールすれば簡単至極だけど、 ちょっと注意すべき点もある。- インストールは上手く行ってるように見えるのに、
そもそも起動しない、という場合は
- 古い ipython (notebook) や jupyter
のファイルが残っているのが原因、という事がある。
それらで四苦八苦した事がある人は要注意——経験者語る。
いつ入れてしまったのか全く憶えてないが、
/usr/local/share/jupyterというのが有って、これを完全に除いてしまう必要があった。(pve35) fukuda@falcon:~/pve35% rm -rf /usr/local/share/jupyter
-
pip-compile, pip-syncで、Jupyter を入れる時に、 root でやってはいけない。やってしまったら、chown で、owner と group を書換える必要があるが、いっその事、PyVenv の再構築から遣り直した方が早い。
- 古い ipython (notebook) や jupyter
のファイルが残っているのが原因、という事がある。
それらで四苦八苦した事がある人は要注意——経験者語る。
いつ入れてしまったのか全く憶えてないが、
- (多分、余計な制限をつけて動かない環境を増やすのを嫌っての事だと思うが) scipy と pandoc が無くても Jupyter Notebook は起動できる。 が、前述のように、後で文句を言われるので、最初から入れておくのが無難。 (そもそも、これら無しでは Jupyter Notebook は意味がないように思うのだが。)
- 上と逆のケースだが、大元の Python が 3.5.x だと qtconsol はインストールされるが、qtconsol は Jupyter Notebook から使えない。 (qtconsol-4.2.1 は Python-3.5.x に未対応)
- 何故か config file がどこにも無い。どうやら、動くようになってから、
(pve35) fukuda@falcon:~/pve35% jupyter notebook --generate-config Writing default config to: /Users/fukuda/.jupyter/jupyter_notebook_config.py
とやって作るという事らしい :-(
使ってみた
フィルタの設計はやっかいなものである。 アナログ、デジタルにかかわらず、 フィルタ定数の最適化が難しいのは言うまでもないが、 それ以前に「それらしい形」にさえなってくれない、なんて事がよく有った。 (要は、定数の計算を間違えていた?) なので、今回とあるフィルタの設計が必要になって、少々気が重かったのだが……
幸い scipy.signal に IIR フィルタの設計モジュールが有る事を知り、
早速 iPython で試してみると、これがまた非常に良くできていて、b, a
係数の計算と最適化は一発。これだけでも感涙モノだけど、
問題は減衰量と Q 値のトレードオフで、要求が微妙で厳しい上に、
与えるパラメータの数(設計の自由度?)が非常に多いので、
膨大なカット&トライが必要になる——iPython でさえ大変かも。
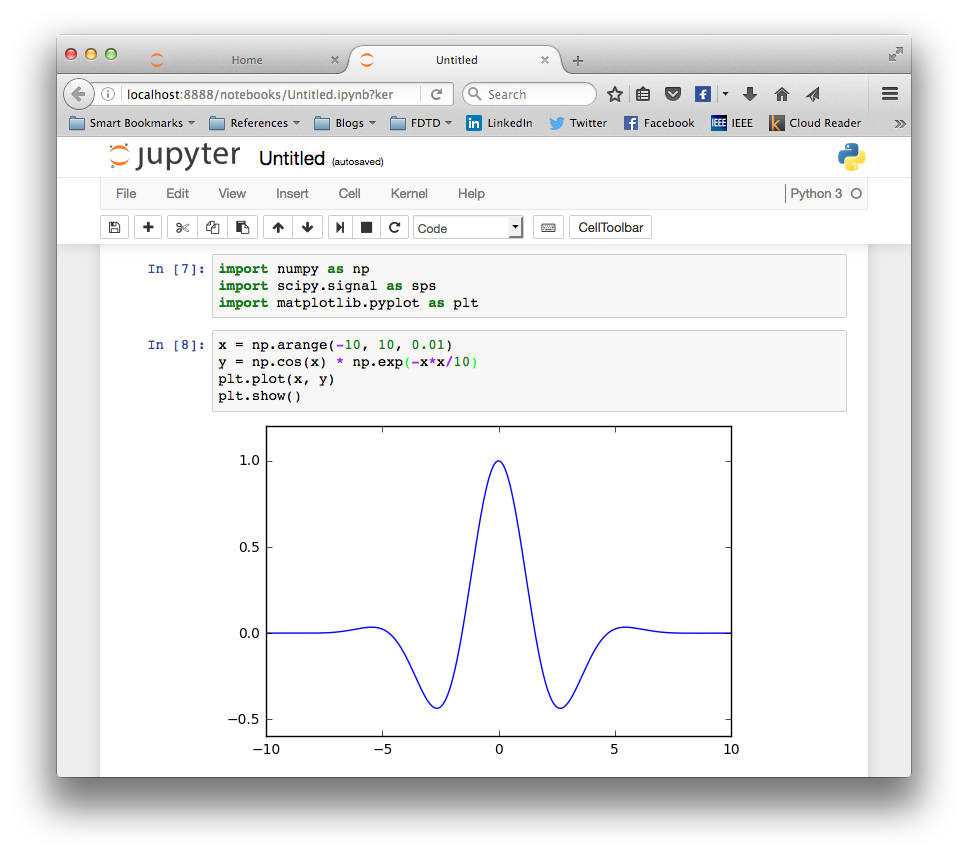
で、思い立って Jupyter を使ってみる事にしたのだった。
やってみるとこれが大正解。 設計から周波数特性確認、実信号に対する応答を見る、 までのかなり長いプロシージャを間違いなく繰返すのはしんどい作業だが、Jupyter だとそれが大分容易になる。
実際にやった仕事(をかなり簡略化したもの)を、 ここに上げて置く。
Notes
系統立った使い方は、上に挙げたサイトを見るのが最も近道であるが、 (自分用に) それに付け加える Notes:- Python/iPython の readline の一部の機能が使えない (Ctrl-R, Ctrl-P 他)。少々いらつくが、「cell 単位の編集」に慣れて、かつ、Shift-NL に加えて、Ctrl-NL (実行して結果を表示するが、セル内に止まる) を活用すれば、それ (readline の非力さ) を補って余り有るだろう。
- たとえ非常に薄いラッパーでも、関数として定義しておいて、 カット&トライの間中常にその関数を使う事にすれば、 ケアレスミスの確率をかなり下げられる。
- それでも、長い Note を延々と修正していると、 つい辻褄が合わなくなる事がある。(例えば、異なるセルに重複した def が有った場合、 下の方の cell の定義がそれ以降適用されるのではなく、 後に実行した方が名前空間に登録され使われる。) なので、一段落したら (つまりセーブする前に)、常に [Kernel] → [Restart & Run All] とやって、整合性を確認しておくのが良い。
- iPython でとても有効だったクラスやアトリビュートの補完が何故か効かない。 (これはドキュメントをもっとよく読めばどこかに書いて有るような気がする。)
まとめと感想
- matplotlib に MathJax に iPython…… それぞれ気に入っていて、よくお世話になっているので、 合わせたら素晴しく強力なツールになりそうだ、 というのは想像に難くないが、 Notebook がこれらを全部合わせて、 しかも「ウェブアプリ」にしたのは確かに素晴しいアイディアだと思う。
- matplotlib でファイルに出力するのが困難、だとか、readline が不完全とかの不満も有ったが、使ってみれば (よく考えてみれば) これらは欠陥ではなくてそもそも不要な機能なんだろうと思うようになった。
- PyVenv と PyPI (pip-tools) のおかげで、Jupyter のインストールもバージョン管理も非常に楽になった。 なのに、最新のドキュメントでも、Anaconda を使ってのインストールがディフォルトになっている…… これは考え直した方が良いのでは?
- それにしても、(上の点も含めて) ドキュメントがもうちょっと何とかならんか……。
2016-09-10 (Sat): Jupyter (iPython Notebook)
Jupyter (旧称 iPython notebook) を一言で言うと、Python のコード入力・実行・結果(出力)表示を、 紙のノートブックに書くようにひとまとめにできるシステム、とでもなろうか?そんな事は iPython でもできる……確かに。 しかし、Jupyter はそれに加えて、Python のコードや出力に並べて Markdown による文章の入力や、matplotlib によるグラフをインラインで表示できる。 特に後者のメリットが大きい。
Jupyter 以前の苦闘
Python を長く使っているという点では人後に落ちないと自負しているが、 使う開発環境はそれ程進歩していない。IDLE や、Emacs の Py-shell、 はたまた iPython 等も試したが、いつの間にか、Zsh から起動する「Python プロンプト (interactive shell)」に戻って来ていた。そんな不精者が重い腰を上げて iPython に移行する事になった切っ掛けは、NumPy-1.10.0 と Python-3.5 で、"A @ B" が行列同士の掛け算を表わすようになった事かも。 ほぼ同時に、MacPorts でも Python-3.5 を配布するようになった事もあり、 あっちこっちで環境を「近代化」 したが、そのついでに、iPython も使い始めたのだった。 (しかし、実は "A @ B" はそれ以降然程使っていない。:-)
その時に書いた「不満」もまだ一部残っているが :-p まあ、なんとか今も、iPython を使い続けている。 (不満が残っているのに、使い勝手がまた最近変わったようだ。) しかし、iPython を使っていると当然 iPython Notebook に興味が湧いてくるのだが(皆に勧められるし)、 これがどうもうまく行かない。PyVenv (の pip によるバージョン管理) は、環境の管理という面では大きな改善をもたらしたが、 残念ながら、iPython Notebook の機能だけは、 そもそもまとに立ち上がるようにできなかった。
Anaconda も勧められて、ちょっとやってみたが、こちらも惨敗に終った。
PyVenv と Jupyter
その後も何度か挑戦してみては撃退されていたが、- PyVenv (と PyPI) が改善され、pip-tools まわりの不具合が解消された事、
- その PyPI に、Jupyter パッケージが加わった事
実はこれ、ちょっと前の話だが、 インストールの手順の一部を記録し忘れていたしたような気がして、 ここに書くのを遠慮していた。 しかし、今週に入って、人様の OSX-10.11.6 に、まさに一から (MacPorts から) インストールしてみて、あっさりうまく行ったので、 書き残す気になった。(その「一から」書いているけど、 既に途中のステップを卒業している人は、スキップしても大丈夫。)
まずは、 MacPorts のサイト の Quick Start の一覧の中から、自分の OSX バージョンに合った pkg をダウンロードしてきてインストール。
以降は、Terminal.app から実行する。(Terminal で走る zsh/bash の設定は端折る。ここでは Zsh を使っているが、ディフォルトの Bash でも問題無い。)
fukuda@hawk:~% sudo xcode-select --install fukuda@hawk:~% sudo port install python35 fukuda@hawk:~% pyvenv-3.5 pve35 fukuda@hawk:~% cd pve35 fukuda@hawk:~/pve35% . bin/activate (pve35) fukuda@hawk:~/pve35% (pve35) fukuda@hawk:~/pve35% pip install pip-toolsここまでで、Xcode Commandline Tools と PyVenv のインストールは完了。以降、この環境に、Jupyter をインストールする。
~/pve35/requirements.in に
pip-tools numpy matplotlib scipy jupyter pandocと書いて、
(pve35) fukuda@hawk:~/pve35% pip-compile (pve35) fukuda@hawk:~/pve35% pip-syncとやると、依存関係をちゃんと解決して大量の他のモジュールと共に Jupyter のインストールは完了する。(但し scipy と pandoc の依存関係は無視されるようで、これらを
requirements.in
から省いていると、インストールされず、後で文句を言われる。)
以下のようにして、Jupyter を起動する。
(pve35) fukuda@hawk:~/pve35% jupyter notebook [I 12:42:51.603 NotebookApp] Serving notebooks from local directory: /home/fukuda/pve35 [I 12:42:51.603 NotebookApp] 0 active kernels [I 12:42:51.603 NotebookApp] The Jupyter Notebook is running at: http://localhost:8888/ [I 12:42:51.603 NotebookApp] Use Control-C to stop this server and shut down all kernels (twice to skip confirmation).と表示され、一方で Firefox が起動され (これも、Well-hidden-truth だが :-) ) [New] ボタンをクリックして、 Python3 を選ぶと、Unknown セッションが新「カーネル」の上で始まり、 以下のような、iPython のプロンプトが表示される。 以下、通常の iPython におけると同様、 コマンド入力とその処理結果が表示される。 とりあえず、簡単なグラフを描かせてみた。
2016-08-20 (Sat): 宅外サーバのメンテナンス
DigitalOcean の VPS (つまりはこの otacky.jp サーバ) はその後も頗る好調で、 7ヶ月間というもの問題らしい問題は何もない。 ならば「動いているものは弄るな」の原則に従うのがプロというものだろうが、 ついついオタク心が……最新カーネルを使えるようにする
Ubuntu-14.04 をインストールしてから、すぐにβ版の 16.04 にしておき、正規リリース後正式版に…… という目論見は MVware Fusion 他ではうまく行った。 しかし、肝心の DigitalOcean ではダメ。カーネルだけが何故か最新版にならない。 16.04 on kernel-3.13.0-71 という変態的状態のまま。(16.04 のカーネルは最初から 4.4.0-xxx。)DigitalOcean の Wiki での Q&Aによると Ubuntu-14.04 までは、実際に使用される kernel は control panel からのみ制御・選択可能 (apt-get update/upgrade で kernel を upgrade しても、はたまた、ディストリビューションを 16.04 にしてもこれは変わらない。) という事らしい。
それでは、という事で、その control panel から、 最新のカーネルを選んでみたら、ブートはするが eth0 デバイスが作られてい ない……びびってしまって、即 original kernel に戻した。
Wiki で「16.04 のクリーンインストールから始めるのが吉」と言われたこともあり、 ちょろっとやりかけたが、Mail 関連のシステム (Postfix, Mailman, Dovecot) をポートしてテストするのが大変 (Host Certificate が絡むので余計!)。 で、挫折——新しい droplet (digoc03) を三ヶ月の店晒しにしてしまった……。
もう半ば「変態状態のままで、18.04 まで行こうか」と諦めかけていたのだが、 店晒しの droplet をすっぱり諦めてしまう前に、 現行 droplet (digoc02) で「奥の手」を試みる事にした。
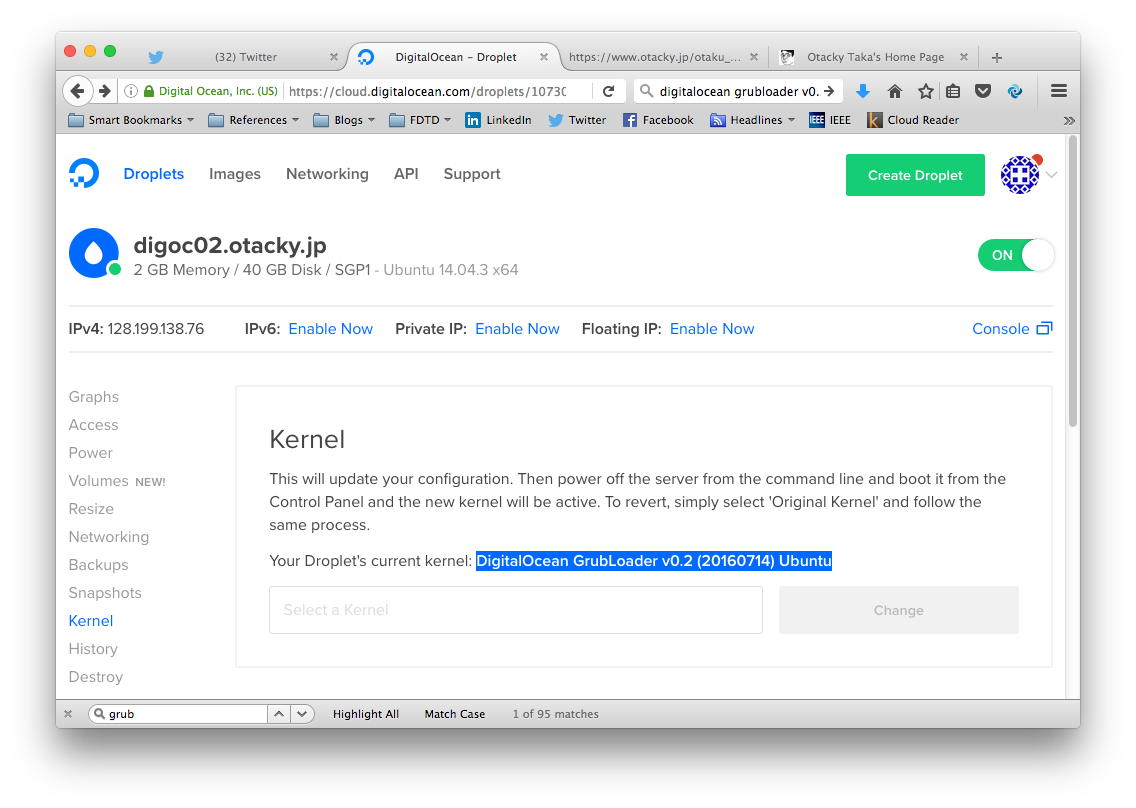
- Control panel の Droplets => Kernel へ行き、drop-down menu で、'DigitalOcean GrubLoader v0.2 (20160714) Ubuntu' を選ぶ。
- digoc02 へログインして、
# shutdown -h now - Control panel から Power On
fukuda@falcon:~% ssh otacky.jp
Welcome to Ubuntu 16.04.1 LTS (GNU/Linux 3.13.0-71-generic x86_64)
.....
だった、'System information' が、この変更の後では
fukuda@falcon:~% ssh otacky.jp Welcome to Ubuntu 16.04.1 LTS (GNU/Linux 4.4.0-34-generic x86_64) * Documentation: https://help.ubuntu.com * Management: https://landscape.canonical.com * Support: https://ubuntu.com/advantage System information as of Fri Aug 19 18:05:03 JST 2016 System load: 0.07 Processes: 147 Usage of /: 27.5% of 39.25GB Users logged in: 0 Memory usage: 10% IP address for eth0: 128.199.xxx.xxxx Swap usage: 0% Graph this data and manage this system at: https://landscape.canonical.com/ 13 packages can be updated. 8 updates are security updates. No mail. Last login: Fri Aug 19 16:50:07 2016 from 116.58.xxx.xxx fukuda@digoc02:~%となった。 案ずるより生むが易し……なぜもっと早くやらなかったんだろ、とも思うが、 BootLoader がアップデートされたのが、ついこのあいだ (7月) だから、これまで待って正解だった、と思う事にしよう。
ちなみに、こうしても、Ubuntu-16.04 を最初からインストールしたのと完全に等価ではない。 ('internally managed' になってない、という意味。) 変更後
のように Kernel ペインが表示されるが、 'internally managed' であれば、同ペインは dropdown menu の代わりに、The kernel for this Droplet is managed internally and cannot be changed from the control panel.と表示される。
ちょっと気にはなるが、# apt update/upgrade で更新される
kernel が走るのだから、18.04 LTS まではこれで行く事にする。
Certificate の更新
Let's Encrypt の certificate は三ヶ月毎のリニューアルが必要だが、 それを簡単にしようと、態々certbot-auto
で、登録をやり直したのだった。
その後すぐ更新を試みたが、残り期間が一ヶ月を切らないと、
更新コマンドを受け付けないとかで、最終的な確認はできていなかった。
(その時は、--force-renew が効かなかった。)
そのうちに、(案の定) すっかり忘れてしまっていて、 また失効させるところだったが、有難い事に、Let's Encrypt さんからメールで「更新のお知らせ」が来た。(一時間おきに、計 3 通も :-)
早速、やってみる。
fukuda@digoc02:~/certbot% ./certbot-auto renew
Requesting root privileges to run certbot...
/home/fukuda/.local/share/letsencrypt/bin/letsencrypt renew
[sudo] password for fukuda:
-------------------------------------------------------------------------------
Processing /etc/letsencrypt/renewal/www.otacky.jp-0001.conf
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
new certificate deployed without reload, fullchain is
/etc/letsencrypt/live/www.otacky.jp-0001/fullchain.pem
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
Processing /etc/letsencrypt/renewal/www.otacky.jp.conf
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
new certificate deployed without reload, fullchain is
/etc/letsencrypt/live/www.otacky.jp/fullchain.pem
-------------------------------------------------------------------------------
Congratulations, all renewals succeeded. The following certs have been renewed:
/etc/letsencrypt/live/www.otacky.jp-0001/fullchain.pem (success)
/etc/letsencrypt/live/www.otacky.jp/fullchain.pem (success)
うまく行ったようだが、ちょっと問題が……。xxx.conf
が二つあるのはともかく、その内容 (ホスト名) が重複している。これで良かったっけ?
不安は残るが、とりあえず動作確認:
- www.otacky.jp, www.waremo.com へ、https でアクセス → OK
- smtp.otacky.jp, imap.otacky.jp へ、submission (port: 587), imaps (port: 993) でアクセス → OK
- otacky.jp から gmail.com へ、submission (port: 587) → OK
後は、これを crontab に移して自動化する。$ certbot-auto
は、途中で sudo のパスワードを要求するので困難が予想されたが、root
権限で実行すれば、それもない事がわかり、
次のようにして動くようになった。
fukuda@digoc02:~% sudo crontab -u root -e #1) crontab: installing new crontab #2) fukuda@digoc02:~% sudo crontab -u root -l ..... # m h dom mon dow command 0 4 * * 1 /home/fukuda/certbot/certbot-auto renew #3) fukuda@digoc02:~%ここに、
- #1) sudo と -u root 両方が必要。このコマンドで、nano が立ち上がるので、下の -l で示されているような内容をタイプインし、 ^w, ^x としてセーブ・終了。
- #2) nano から抜けるだけで、root の crontab がインストールされ、起動される。
- #3) 毎週月曜日の午前 4 時にリニューアルを試みる。
--force-renew
付きで起動されるように設定して、つまり
*/2 * * * * /home/fukuda/certbot/certbot-auto renew --force-renewとして試験してみたところ、 ちゃんと root@otacky.jp に「リニューアル成功」のメールが送られて来た——今度は
--force-renew が効いたようだ。
(勿論、このまま放置してはいけない。)
2016-08-13 (Sat): FreeFem++ と 4 探針法(その 2)
以下、単位のつかない寸法・距離は、プローブ間の距離を 1.0 とする相対値。 また、プローブの電極 (探針) は左から 1, 2, 3, 4 と番号を振り、 1, 4 が「電流プローブ」、2, 3 が「電圧プローブ」であるとする。Sanity Check (その 2)
先回の Sanity Check では、電流プローブの半径 r0 を
- r0 = 0.2: 無限大のサンプルで解析的に求めた F の理論値 4.532 に対して、-3%
- r0 = 0.1: 80 x 50 mm2 のサンプルで JIS が与える「F の理論値」 4.147 に対して、-2.1%
今回、それぞれのプローブの周りに半径 0.2 の(擬似)バウンダリーを置くと、 上記のメッシュ作製時の問題が抑制される事が解ったので、 プローブの半径を 0.0005 まで小さくして、上記の 2. の条件で、F の相対誤差を -0.34% まで下げる事ができた。
電極が有限な寸法を持つ場合への拡張
ところが、4 探針法用のプローブの中には、先端が針状もしくは球状ではなくて、 かなり大きい扁平な円盤状になっているものがある。 これは柔くて不均一な資料(例えば織布)には好都合であるが、 上記のシミュレーションから得た F 値をそのまま適用できないのは明らか。上記のサイズ (半径 1 mm) は、電流、電圧プローブに共通であるが、 電流プローブは(電圧を固定した)「ディリクレ境界」で表わしているので、 この寸法を変えるのは簡単。一方、電圧プローブの方は、 シート上の一点の電位を計る (メッシュの節点の値から内挿する) 事で代用しているので、拡張のしようがない。
最初に思いついたのは、電圧プローブもディリクレ境界 (C2, C3) で表わす事。 すなわち、 $$ u = +1 \quad (\text{on C1}) \\ u = +\phi \quad (\text{on C2}) \\ u = -\phi \quad (\text{on C3}) \\ u = -1 \quad(\text{on C4}) \\ $$ 等としておいて、$\phi$ を変分法で求める事。 フロート電極の電位をこうやって FEM の中で変分法で求める方法は確かにどこかで見た気がするのだが、 今どうしても見付からない……
とすると、実際に電圧プローブを C2, C3 で囲まれる領域内が導体 (導電率 $\sigma_s$) で埋められているという「電極」で定義する他無さそうである。即ち、 試料全体 $\Omega$ を、C2, C3 の境界で囲まれる領域 $\Omega_2$, $\Omega_3$ と、それ以外の領域 $\Omega_0 = \Omega \setminus \Omega_3 \setminus \Omega_3$ (A \ B は A と B の差集合を表わす) に分割して、 $$ \begin{align} -\nabla^2 (\sigma_s u) & = 0 \quad (\text{in} \, \Omega_2 \cup \Omega_3)\\ -\nabla^2 u & = 0 \quad (\text{in} \, \Omega_0)\\ u & = +1 \quad (\text{on C1}) \\ u & = -1 \quad (\text{on C4}) \\ \end{align} $$ つまりは、境界 C2, C3 は自由境界 (Neumann) 条件としている。
これを、FreeFem++ のコードに落すと
float sigmam = 1e+5;
int metal2 = Th(-0.5, 0).region; // *1)
int metal3 = Th(+0.5, 0).region;
int sheet = Th(0, 0).region;
Vh uh,vh; // uh: potential
Vh sigmas = sigmam * ((region == metal2) + (region == metal3))
+ 1.0 * (region == sheet); // *2)
problem Electro(uh,vh) =
int2d(Th)(sigmas * ( dx(uh)*dx(vh) + dy(uh)*dy(vh) ))
+ on(C1,uh=1)
+ on(C4,uh=-1) ;
とできる。ここに、
- *1) Th().region は、boundary で区切られた領域の固有の名前 (整数)を返す。
- *2) global 変数 region は、その点での領域名 (番号) を持っていて、 かつ、'==' 演算子の結果は、True で 1, False で 0 を返すので、 この式全体では、metal2, metal3 リージョンでは sigmas = 1.0e+5, それ以外では sigmas = 1.0 となる。
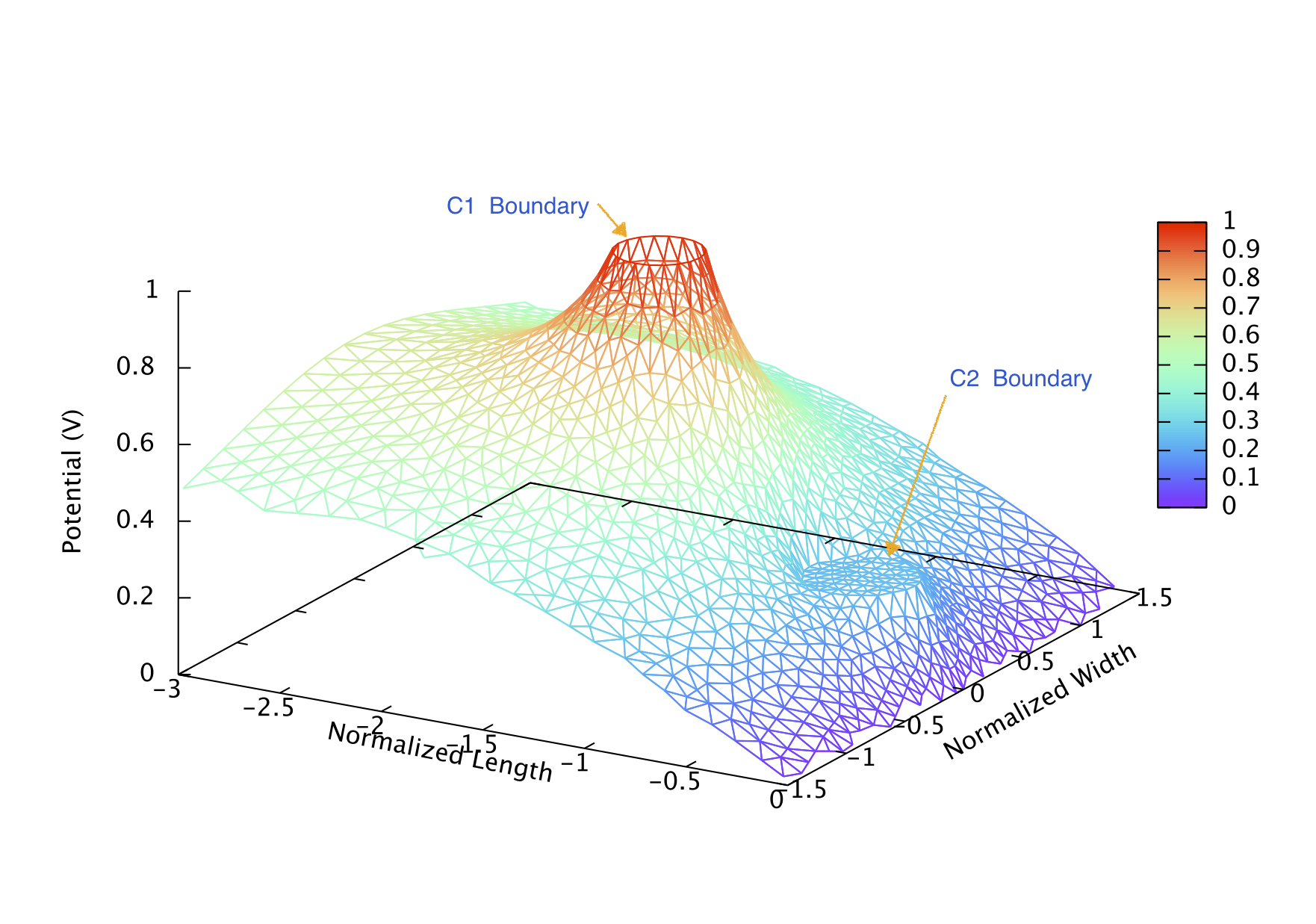
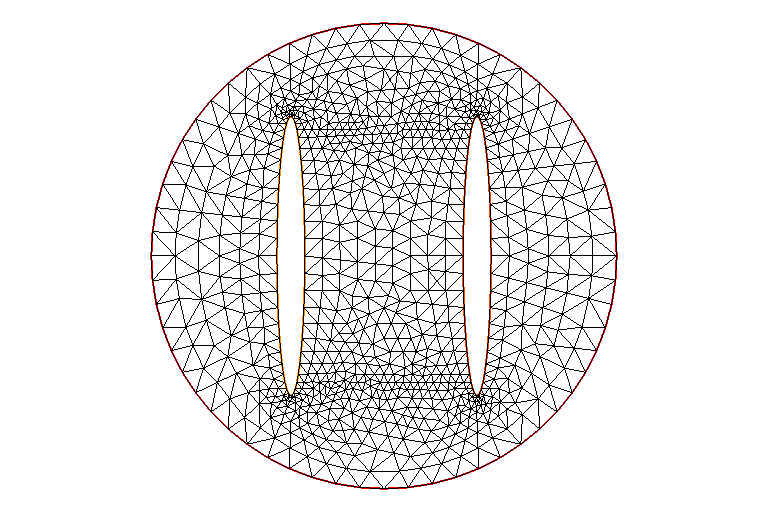
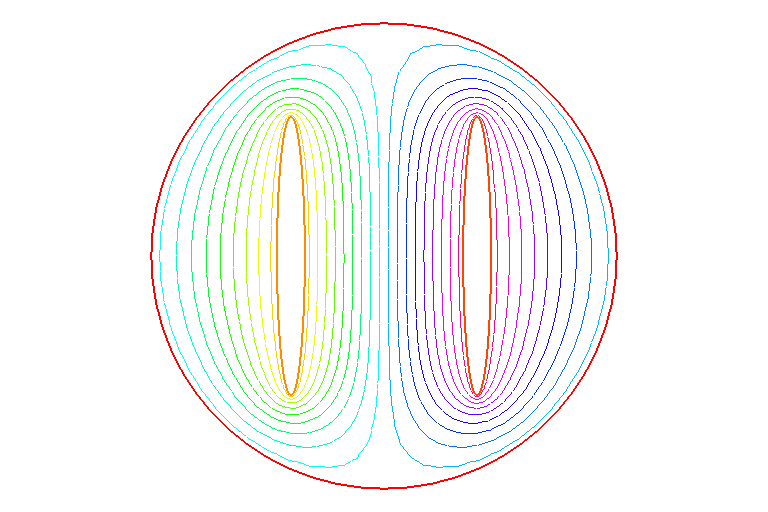
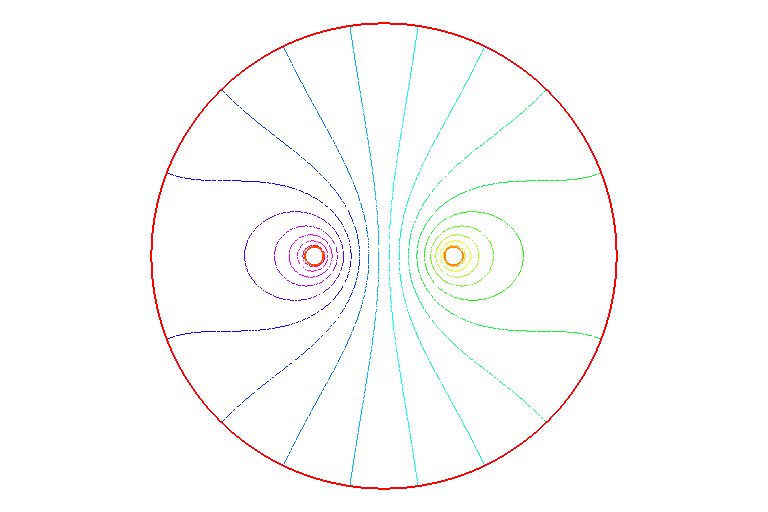
C2/C3boundary に囲まれた領域で電位がフラットとなっている事がよく解る。 (Nmesh は、Cn の境界上の刻み数) これをさらに詳細に表わすために等電位線の分布を下に示す。
等電位線がほぼ境界に沿っている場合 (C1, C4) は、 刻み幅はそれ程電場分布に影響しないが、C2, C3 のように、 他の要因 (この場合は C1, C4) で作られる電場の中に強制的に置かれるような場合はそうは行かず、 Nmesh は (また周囲の境界の刻み数も) 4 倍程にしないとかなりの誤差を含む事が解る。
F の計算
上で述べたような「スキーム」を使って、 先端が円盤になっているプローブを使った場合の 4-探針法の変換係数 F を算出してみた。後者のプローブは、探針間隔 5 mm で、 探針の先端の円盤の半径は 1 mm とした——つまり、r0 = 0.2。
//
load "Element_P3"
real r0 = 0.2;
real L = atof(ARGV[2]); // L = 16
real W = atof(ARGV[3]); // W = 10
real sigmam = 1.0e+5;
int nmesh = 80; // atof(ARGV[4]);
border C01(t=-1, 1) {x = -0.5*L; y = 0.5*W*t; }
border C02(t=-1, 1) {x = 0.5*L*t; y = 0.5*W; }
border C03(t=-1, 1) {x = 0.5*L; y = -0.5*W*t; }
border C04(t=-1, 1) {x = -0.5*L*t; y = -0.5*W; }
border C1(t=0,2*pi) { x = -1.5 + r0 * cos(t); y = r0 * sin(t); }
border C2(t=0,2*pi) { x = -0.5 + r0 * cos(t); y = r0 * sin(t); }
border C3(t=0,2*pi) { x = +0.5 + r0 * cos(t); y = r0 * sin(t); }
border C4(t=0,2*pi) { x = +1.5 + r0 * cos(t); y = r0 * sin(t); }
real current, currentC1, currentC4;
real V2, V3;
mesh Th = buildmesh(C01(-140) + C02(-200) + C03(-140) + C04(-200)
+ C1(-nmesh) + C2(nmesh) + C3(nmesh) + C4(-nmesh));
// plot(Th, ps="4probe_square_mesh.eps", wait=true);
fespace Vh(Th, P3);
int metal2 = Th(-0.5, 0).region;
int metal3 = Th(+0.5, 0).region;
int sheet = Th(0, 0).region;
Vh uh,vh; // uh: potential
Vh sigmas = sigmam * ((region == metal2) + (region == metal3))
+ 1.0 * (region == sheet);
problem Electro(uh,vh) =
int2d(Th)(sigmas * ( dx(uh)*dx(vh) + dy(uh)*dy(vh) ))
+ on(C1,uh=1)
+ on(C4,uh=-1) ;
Electro;
// plot(uh, ps="four_probe_potential_tmp.eps", wait=true);
currentC1 = int1d(Th, C1) (N.x*dx(uh) + N.y*dy(uh)) ;
currentC4 = int1d(Th, C4) (N.x*dx(uh) + N.y*dy(uh)) ;
V2 = uh(-0.5, 0);
V3 = uh(0.5, 0);
cout << L << "\t";
cout << W << "\t";
cout << currentC1 / (V2 - V3) << "\t";
cout << nmesh << endl;
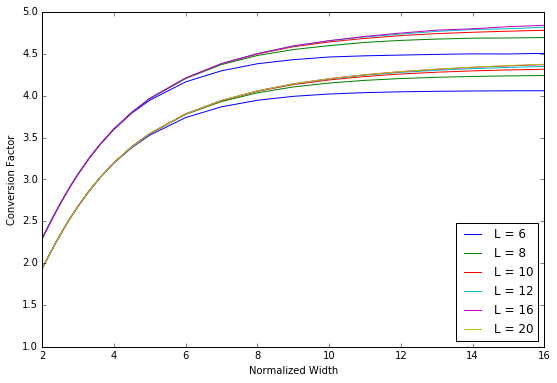
このコードを使って、種々の L, W の組合せについて F を計算し、
L をパラメータとしてプロットすると下図のようになる。
なお、下側の曲線群は、従来の (針状) 探針のプローブの結果である。
結論
探針の試料とのコンタクト面が有限の広がりを持つ場合、実測した $R_0$ から、 シート抵抗を求めるための変換係数 F は、 針状の探針の場合とかなり違ったものになる。 典型的には、L = 16 (80 mm), W = 10 (50 mm) の試料サイズの場合、探針間隔 5 mm の針状探針では F = 4.203 だったものが、 直径 2 mm の円盤状探針では、F = 4.657 と約 10% 増しとなる。2016-07-09 (Sat): MathJax 再訪
MathML から MathJax へ
MathML は HTML5 の一部の筈なんだけど、どうも (ブラウザの) 機種依存性が有って具合が悪い。という事で、半信半疑で MathJax に移行してみたが、これがなかなかよくできている。 特にマトリックスの表記については 前に示したように格段に見易くなる。なので、先週の FEM に関する記事でも、深く考える事なく「数式は MathJax で行こう」となった。が、やってみるとこれが大変。 行列やベクトルの表記については (直近で四苦八苦した事もあり) 何とか憶えているが、 '$\nabla$' や '$\iint$' などについては、どう書くのか見当もつかない……
が、たまたま MathJax basic tutorial and quick reference というページに要領よく纏めてあるのを見付けた。 このページ、典型的な式やシンボルを右クリックして、[Show Math as] → [Math ML Code] とか [Show Math as] → [TeX Commands] などを選ぶと、それぞれ MathML, TeX のコードを表示してくれる、という優れもの。
MathJax の TeX-AMS Config
暫くそれに倣って、MathML で微分方程式他を書いていたが、 TeX 表記に比べて何とも長ったらしいなぁという思いが募る。 そうこうするうちに、ふと、 「そもそもチュートリアルの中で何で TeX のコマンドが本文内で先に書いてあるんだ?」という素朴な疑問が…… で、最初の方を良く読むと、MathJax は MathML のコードを解するのと同様、TeX コードも解してレンダリングしてくれるんだとか。 むしろ、そっちを使う事を前提のチュートリアルらしい…… (たはっ)。ともあれ、これは素晴しい……コード (コマンド?) が格段にコンパクトになり、何より 「これ、どんな風に書くんだっけ」にすぐ見当がつく! (LaTeX は殆んど憶えて ないけど、それでも!)
この機能を使うのは簡単で、MathJax.js を MM_HTML (MathML_HTML) ではなく、 TeX-AMS_HTML を解するバージョンを使う方に変更するだけ。つまり
<!-- script type="text/javascript"
src="https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=MML_HTMLorMML">
</script-->
<script type="text/javascript"
src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS_HTML">
</script>
<script type="text/x-mathjax-config">
MathJax.Hub.Config({ tex2jax: { inlineMath: [['$','$'], ["\\(","\\)"]] }});
</script>
<!-- meta http-equiv="X-UA-Compatible" CONTENT="IE=Edge" -->
x-mathjax-config はインライン表示のマーカー (デリミタ?)
を示している。つまり、$$...$$ のようにコードを囲めば、MathML で言う
'block display mode'
で表示され、これがディフォルトであるが、$...$ とすれば、'inline
mode' になる (高さを押えた表記になって、文中に埋め込まれる) という事。ま
た、最後の
<meta> は IE
のための配慮であるが、先程試したところによると、
無くても問題なさそうだった。(IE11 で確認。)
TeX-AMS と MathML コードの比較
で、TeX-AMS コードで書ければどれくらい嬉しいか、という比較。例えば、先に出てきた $$ \iint_{\Omega} \left\{ \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \frac{\partial v}{\partial y} \right\} dxdy = 0 $$ を表わすのに、TeX-AMS ならば
$$
\iint_{\Omega} \left\{ \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} +
\frac{\partial u}{\partial y} \frac{\partial v}{\partial y} \right\} dxdy = 0
$$
で済むが、MathML だと
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<msub>
<mo>∬</mo>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">Ω</mi>
</mrow>
</msub>
<mfrac>
<mrow>
<mi mathvariant="normal">∂</mi>
<mi>u</mi>
</mrow>
<mrow>
<mi mathvariant="normal">∂</mi>
<mi>x</mi>
</mrow>
</mfrac>
.....
<mo>=</mo>
<mn>0</mn>
</math>
のようになってしまう。(実際にはもっと長い)
まとめ
これはもう、MathJax の TeX-AMS_HTML で行くしかないだろう。一方で「MathML で書いておいて、当面 MML_HTML で表示させる事にすれば、後々純正の MathML がきちんとサポートされた時、 そっちへスムースに移行できる」という「目論見」を諦める事になるが、 しかし、そもそも、この先 MathML で数式を書く気になるだろうか。(各ブラウザの MathML サポートが進むか、という問題も有るし。)
と同時に、何でもかんでも XML のように「厳密」に書く事や、 「完全性」に拘るのは「なんだかなぁ」 と思えてきたのだった——実は以前からそう感じている。
2016-07-02 (Sat): FreeFem++ と 4 探針法
シート抵抗 (表面抵抗率)
抵抗率の測定に難しい事はなにもない筈、なんて高を括っていた。 何しろ新卒として入った某 F 社で (メッキ工場での研修は除いて) 最初にやらせてもらった仕事が、 Si ウエハの抵抗率の測定だった……その時代でさえ、4 探針プローブをあてれば、 抵抗値が自動表示されたように思う。但しその時は、 形状の影響の補正なんて事は全く念頭になかった (忘れているだけかも)。しかし、話が (不定形のパターンの) シート抵抗の測定原理となると、 この「思い込み」はちょっと甘かったようだ。 まず、それの測定に関する JIS 規格 (K 7194) がどうも「何だかなあ」である。有償(金 1,300 円也) なのにとても不親切でちっとも解らない—— 規格は教科書ではないぞ、と言われそうだが。 まあ、それは措いても、 サンプルを規定通りのサイズに切り出さないといけないのでは、 当面の用途 (生地の上にプリントした導電性インクのシート抵抗を知りたい) には適用できない……。
ともあれ、これは Poisson (Laplace) 方程式に関係している、というおぼろげな記憶は有るので、 これを解くには「有限要素法 (FEM)」を使うんだろうな、という見当はつけていた。 FEM のエンジンは有償無償合わせて沢山有るようなので、 これで、どっかのサイトにそのもずばりの「例題」が有ればもう「こっちのもの」 なんだが……しかし、何故かこんな簡単な問題の例題がどこにもない。 おかげで、けっこうあれこれ FEM のアプリをダウンロードしてはインストールしてみる羽目に……。 そもそも動かないのが結構有る……なんてのは想定の範囲内だったが、 4 探針法はおろか、 シート抵抗を云々している例題が一つも見付からないのには参った。
ともあれ、「Linux/OSX でも動きそう」及び「(電流分布の解析に似た?) 静電界分布の例が有る」という理由で、 FreeFem++ を選んだ。
FreeFem++ を使う
あまり文句を言いたくはないが、このサイトは「洗練されている」とは言い難い……。- FreeFem++-cs とか、FreeFem++ on the Web とかバリエーションが有るのに、その説明が無い。(-cs 版 (統合環境版)は OSX で動かない。)
- 最新版は 4.47 なのに、バイナリ版は 4.46 まで。
- MacOS 向けバイナリは FreeFem++3.46-MacOS_10.10.pkg のような形で供給されているが、このリンクをクリックしたら、 ダウンロードされずに、「表示」されてしまう。 (これは Firefox の設定のせいかも知れない。 Safari と wget では問題無かった。)
- ダウンロードにやたら時間がかかる。(平均すると 140 kbps!)
- インストーラはちゃんと働くが、 アイコンのダブルクリックでは何も立ち上がらない。
気をとりなおして、FreeFem++ を CUI (terminal) モードで使う事にして、再チャレンジしたら、あっさり動いてくれた。 (あっさり、と言っても、インストールされる先が結構バラバラで、 しかもマニュアルと違っているという「ささやかな問題」は有ったが :-)
パッケージについてくる「例題集」には、静電界の例は無かったので、 ドキュメント の 230 ページから切り出した例を static_orig.edp としてセーブ、FreeFem++ コマン ドに食わせてみた。
fukuda@falcon:~% export PATH=$PATH:/usr/local/ff++/mpich/3.46/bin/ fukuda@falcon:~/Work/FEM% FreeFem++ static_orig.edp -- FreeFem++ v 3.460000 (date Ven 8 avr 2016 15:24:50 CEST) Load: lg_fem lg_mesh lg_mesh3 eigenvalue 1 : // area definition 2 : border C0(t=0,2*pi) { x = 5 * cos(t); y = 5 * sin(t); } 3 : border C1(t=0,2*pi) { x = 2+0.3 * cos(t); y = 3*sin(t); } 4 : border C2(t=0,2*pi) { x = -2+0.3 * cos(t); y = 3*sin(t); } 5 : // mesh generation 6 : mesh Th = buildmesh(C0(60)+C1(-50)+C2(-50)); 7 : plot(Th,ps="electroMesh"); 8 : // defining the problem 9 : fespace Vh(Th, P1); 10 : Vh uh,vh; 11 : problem Electro(uh,vh) = 12 : int2d(Th)( dx(uh)*dx(vh) + dy(uh)*dy(vh) ) 13 : + on(C0,uh=0) 14 : + on(C1,uh=1) 15 : + on(C2,uh=-1) ; 16 : // solving the problem 17 : Electro; 18 : plot(uh,ps="electro.eps",wait=true); 19 : sizestack + 1024 =1544 ( 520 ) -- mesh: Nb of Triangles = 1634, Nb of Vertices 896 -- Solve : min -1 max 1 times: compile 0.006596s, execution 0.047968s, mpirank:0で、同時に ffglut というアプリにグラフが表示される。素晴らしい。 ちなみに、以下のグラフは、自動で生成される
*.eps
をプロットしたものではなく、ffglut から直接 TIFF
としてセーブしたものを、PNG に変換したもの。
それまでのジリジリするような、「先の見えない状況」から、 一挙に展望が開けた感じがしたので、早速電流分布の問題に挑戦する。
問題定義
本格的な議論はとてもじゃないが覚束無いので、(例によって)類推で何とかしよう……一般的に、領域 Ω が境界 $ \Gamma \, (= \Gamma_1 \cup \Gamma_2,\, \Gamma_1 \cap \Gamma_2 = \emptyset) $ によって囲まれている時 $$ \begin{align} -\nabla^2 u & = f \quad (\text{in}\, \Omega)\\ u & = g_1 \quad (\text{on}\, \Gamma_1) \\ \frac{\partial u}{\partial n} & = g_2 \quad (\text{on}\, \Gamma_2) \end{align} $$ という微分方程式の境界値問題を $$ \iint_{\Omega} \left\{ \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \frac{\partial v}{\partial y} \right\} dxdy - \iint_{\Omega} f v\,dxdy -\int_{\Gamma_2} g_2 v \, d \gamma = 0 $$ という「弱形式」に変形すれば、それをそのまま solver に食わせて、 解を得る事ができる (らしい)。
上の静電界の問題では、$ u(x, y) $ はそのままポテンシャルで、電荷 $q\, (= \epsilon_0 f)$ は存在せず、かつ $u$ の法線方向の微分 (すなわち電場) が規定される境界はない ($ \Gamma_2 =\emptyset $) から、 $$ \begin{align} -\nabla^2 u & = 0 \quad (\text{in}\, \Omega)\\ u & = 0 \quad (\text{on C0}) \\ u & = 1 \quad (\text{on C1}) \\ u & = -1 \quad (\text{on C2}) \\ \end{align} $$ という「問題」に帰着する。 これを、弱形式に適用して (つまり最初の積分だけを残して)、FreeFem++ のコードに落とすと
11 : problem Electro(uh,vh) = 12 : int2d(Th)( dx(uh)*dx(vh) + dy(uh)*dy(vh) ) 13 : + on(C0,uh=0) 14 : + on(C1,uh=1) 15 : + on(C2,uh=-1) ;となる。
int2d() や dx(uh), on(C0, ...)
などの意味は殆んど自明だろう。
u → uh, v → vh の置き換えはコードを見易くするため。
一方媒体が真空ではなく、シート抵抗 $\rho_s (= 1/\sigma_s) $ の導体である場合、面電流密度 $\mathbf i$ は電場 $\mathbf E = -\nabla u $ から $$ -\nabla u = \mathbf E = \rho_s \mathbf i $$ 定常状態では、$\nabla \cdot \mathbf i = 0 $ であり、$\rho_s$ は一様 $(\nabla \rho_s = 0)$ であるから、この場合も $$ -\nabla^2 u = \nabla \cdot (\rho_s \mathbf i) = (\nabla \rho_s) \cdot \mathbf i + \rho_s \nabla \cdot \mathbf i = 0 \quad (\text{in}\, \Omega)\\ $$ となり、problem の積分の項は静電場の場合と同じになる。 つまり、境界条件と合わせて $$ \begin{align} -\nabla^2 u & = 0 \quad (\text{in}\, \Omega)\\ \partial u / \partial n & = 0 \quad (\text{on C0}) \\ u & = 1 \quad (\text{on C1}) \\ u & = -1 \quad (\text{on C2}) \\ \end{align} $$
これらの境界条件を、4 探針法の測定を実現するために
- C0 (測定試験片全体の境界):
これから流れ出す電流すなわち電場の法線成分 $ -\sigma_s \partial u / \partial
n $
は零であるが、ここは
on(C0, u = xxx)の形の境界条件を与えない事で、この条件を自動的に充たす。 - C1 (電流プローブ 1): 電位を +1 V に固定(境界条件)
- V1 (電圧プローブ 1): 電位 u (V1) を測定
- V2 (電圧プローブ 2): 電位 u (V2) を測定
- C2 (電流プローブ 2):電位を -1 V に固定(境界条件)
//
load "Element_P3"
real r0 = 0.2;
real R0 = 5;
border C0(t=0,2*pi) { x = R0 * cos(t); y = R0 * sin(t); }
border C1(t=0,2*pi) { x = -1.5 + r0 * cos(t); y = r0 * sin(t); }
border C2(t=0,2*pi) { x = 1.5 + r0 * cos(t); y = r0 * sin(t); }
//border Ci(t=0,2*pi) { x = 5 * cos(t); y = 5 * sin(t); }
real current, currentC0, currentC1, currentC2;
real V1, V2;
mesh Th = buildmesh(C0(80) + /* Ci(200) + */ C1(-20) + C2(-20));
plot(Th, ps="four_probe_mesh.eps", wait=true);
fespace Vh(Th, P3);
Vh uh,vh; // uh: potential
problem Electro(uh,vh) =
int2d(Th)(1.0 * ( dx(uh)*dx(vh) + dy(uh)*dy(vh) ))
// + on(C0,uh=0) #1
+ on(C1,uh=1)
+ on(C2,uh=-1) ;
Electro;
plot(uh, ps="four_probe_potential.eps", wait=true);
currentC0 = int1d(Th, C0) (N.x*dx(uh) + N.y*dy(uh)) ;
currentC1 = int1d(Th, C1) (N.x*dx(uh) + N.y*dy(uh)) ;
currentC2 = int1d(Th, C2) (N.x*dx(uh) + N.y*dy(uh)) ;
V1 = uh(-0.5, 0);
V2 = uh(0.5, 0);
//currentC2 = int1d(Th, C2)(efh);
cout << "currentC0 = " << currentC0 << endl;
cout << "currentC1 = " << currentC1 << endl;
cout << "currentC2 = " << currentC2 << endl;
cout << endl;
cout << "V1-2 = " << V1 - V2 << endl;
cout << "F = " << currentC1 / (V1 - V2) << endl;
ofstream ff("example3.plt");
for (int i = 0; i < Th.nt ; i++){
for (int j = 0; j < 3; j++){
ff << Th[i][j].x << " "<< Th[i][j].y << " " << uh[][Vh(i,j)] << endl;
}
ff << Th[i][0].x << " " << Th[i][0].y << " " << uh[][Vh(i,0)] << endl << endl << endl;
}
#1) の部分をコメントアウトするかどうかで、境界 C0 で、電位を 0
に強制するか (Dirichlet 問題)、若しくは電位には構わず、
結果として法線方向の電流(電界)を 0 にするか (Neumann 問題) が決まる。
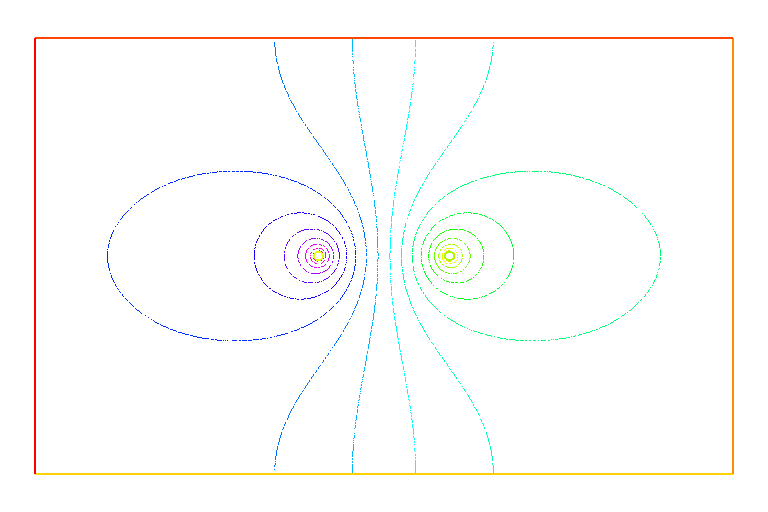
実際結果をプロットしてみると以下のようになる。
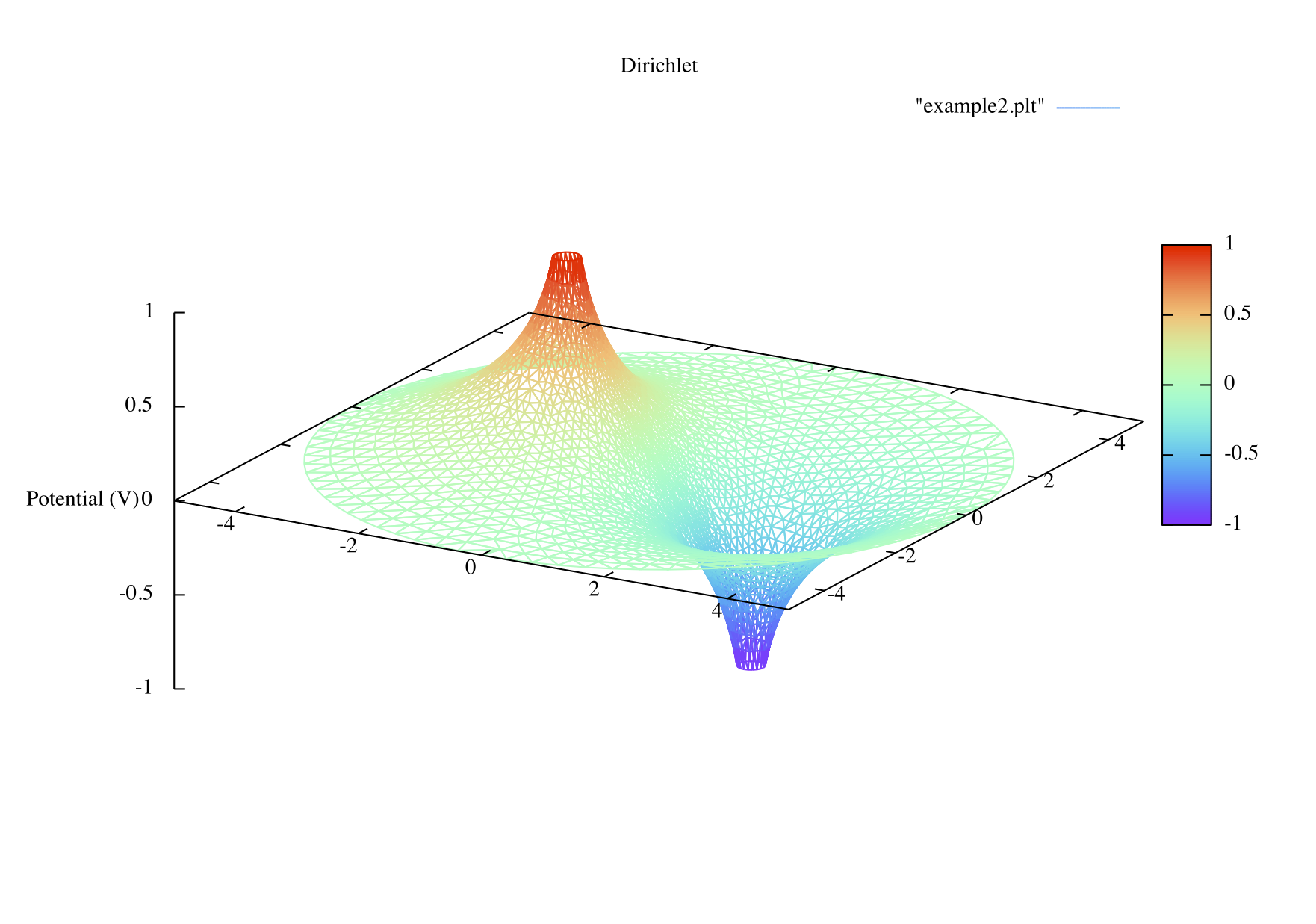
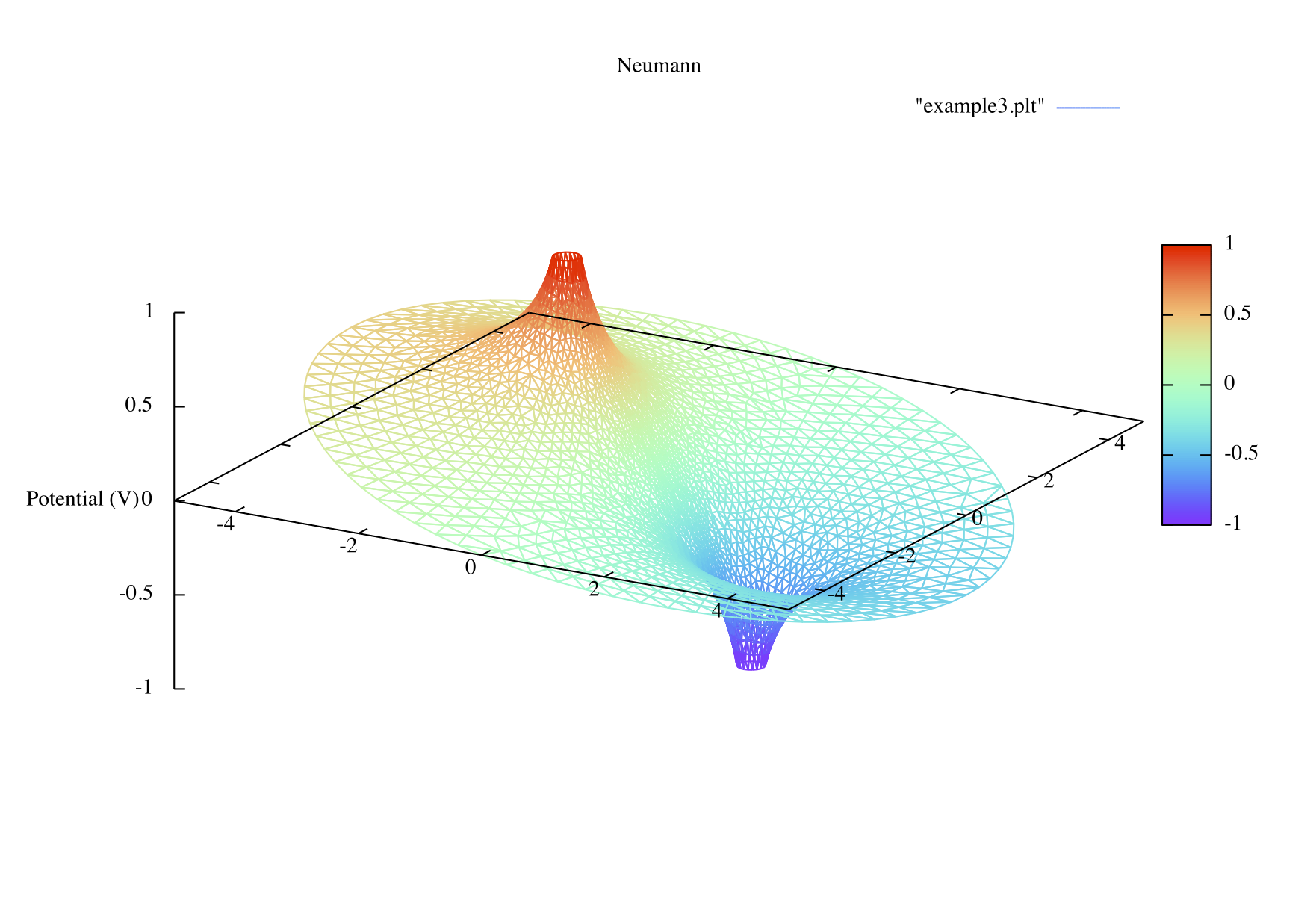
(上側が等電位線、下側がその三次元プロット。)
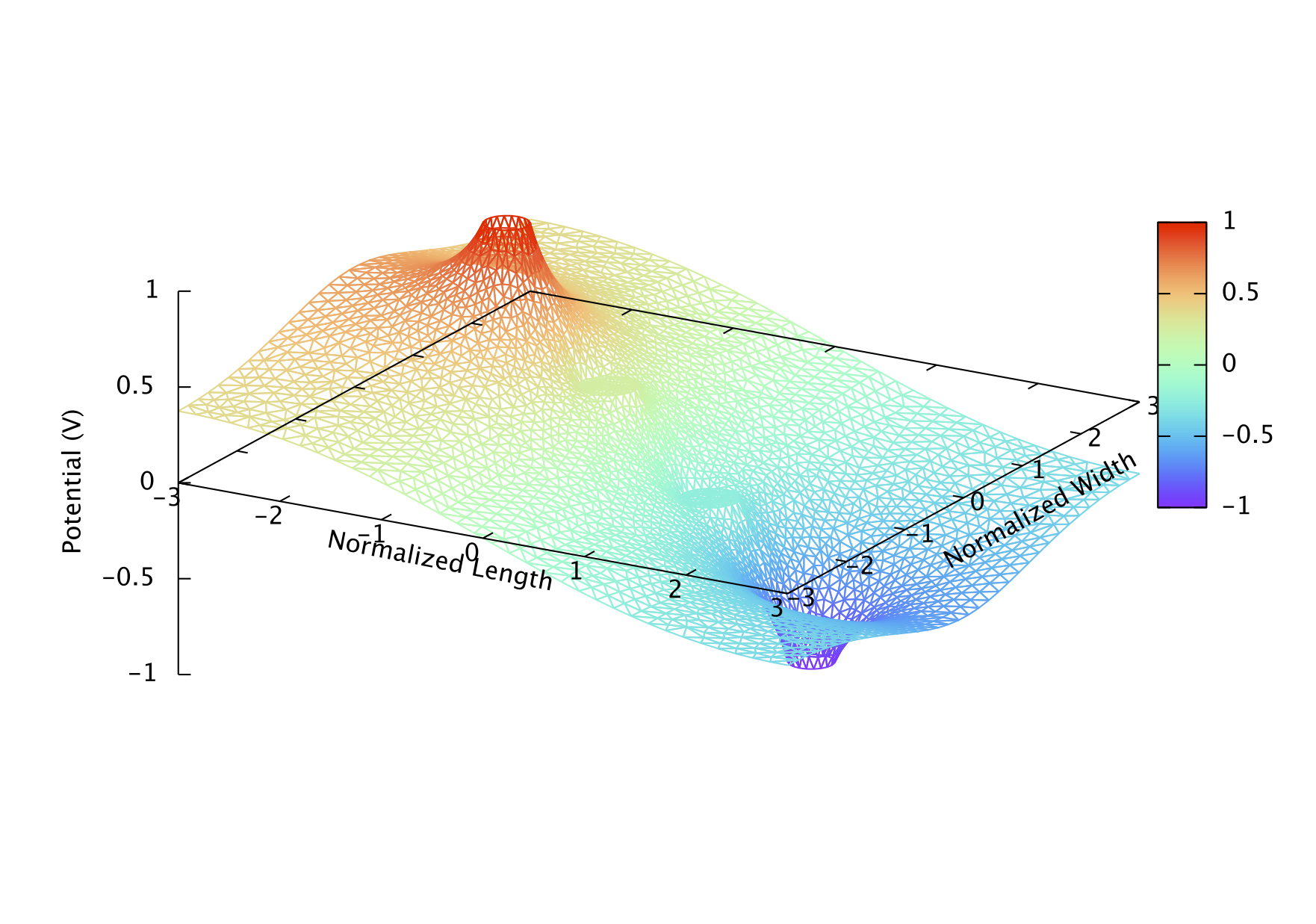
これらの図から、境界 C0 (外周) で確かに予期したような境界条件となっている事がわかる。 すなわち、左側の図では、外周の電位を強制的に 0 に落とした場合は、 外周の法線(半径)方向の電界 (電流) が零にはならず、 左半分では流れ出し、右半分では流れ込む。 一方、右側の図では、(境界条件の通り) 外周部分の法線方向の電界(電流) は零となり、 電流の出入りは無い。(但し、周方向の電流は零ではない。) 言うまでもなく、今回採用した右側の境界条件が、 実際の状況 (サンプルの外周は「自由端」) をより良く反映していると言えるだろう。
Sanity Check (その 1)
少々無理筋を押しているような気もするので、C0 の半径を非常に大きくしてみて、 その場合の F の理論値 $ F = \pi / \log(2) = 4.532 $ と一致するか試してみる。上の epd コードを
.....
real r0 = 0.2;
real R0 = 30;
border C0(t=0,2*pi) { x = R0 * cos(t); y = R0 * sin(t); }
border C1(t=0,2*pi) { x = -1.5 + r0 * cos(t); y = r0 * sin(t); }
border C2(t=0,2*pi) { x = 1.5 + r0 * cos(t); y = r0 * sin(t); }
border Ci(t=0,2*pi) { x = 5 * cos(t); y = 5 * sin(t); }
real current, currentC0, currentC1, currentC2;
real V1, V2;
mesh Th = buildmesh(C0(400) + Ci(200) + C1(-20) + C2(-20));
.....
のように変更し、R0 を 5 から 50 まで変更する。(Mesh の具合をみて
C0, Ci の刻みも変更する。C0 の刻みだけの変更では、
どうしても上手く行かない事があるので、Ci を加えた。)
その結果を下図に示す。
図から明らかなように、サンプルの半径が探針間隔の 30 倍になるあたりで、F 値が極限値 4.397 に逹している。 これは理論値 4.532 に対して、-3% 程小さいだけである。誤差の原因を探るため、R0 は 30 に固定して、r0 = 0.1 とし、各境界における刻みを小さくしてゆくと、F = 4.496 となり誤差は -0.8 % となった。
Sanity Check (その 2)
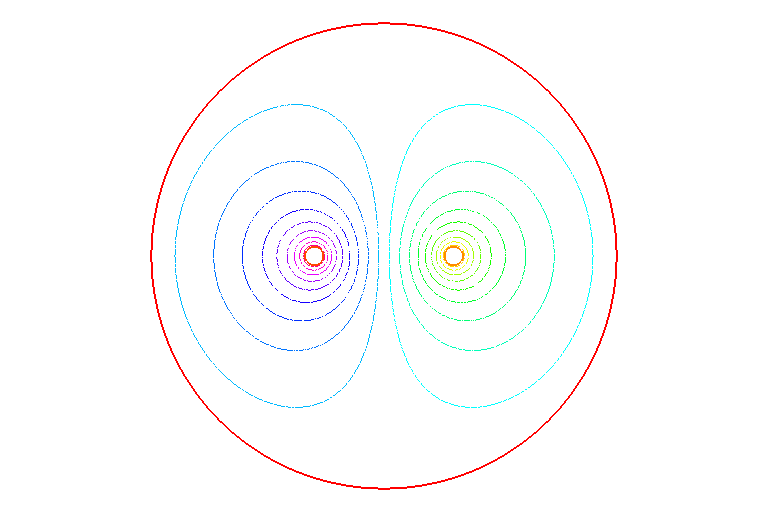
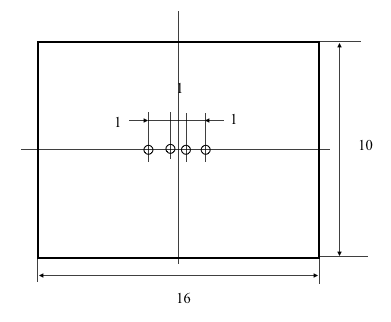
次に、JIS 規格 (K 7194) の F 値と比較する。 同規格でのサンプル寸法 (80 x 50 mm²) を、探針間隔 (5 mm) で正規化した寸法図を以下に示す。 これに対応して上のコードの境界 C0 を長方形にし、 シミュレーションを実施。
fukuda@falcon:~/Work/FEM% FreeFem++ four_probe_rect.epd
-- FreeFem++ v 3.460000 (date Ven 8 avr 2016 15:24:50 CEST)
Load: lg_fem lg_mesh lg_mesh3 eigenvalue
1 : //
2 : load "Element_P3"
3 : real r0 = 0.1;
4 : real L = 16.0;
5 : real W = 10.0;
6 : border C01(t=-1, 1) {x = -0.5*L; y = 0.5*W*t; }
7 : border C02(t=-1, 1) {x = 0.5*L*t; y = 0.5*W; }
8 : border C03(t=-1, 1) {x = 0.5*L; y = -0.5*W*t; }
9 : border C04(t=-1, 1) {x = -0.5*L*t; y = -0.5*W; }
10 : border C1(t=0,2*pi) { x = -1.5 + r0 * cos(t); y = r0 * sin(t); }
11 : border C2(t=0,2*pi) { x = 1.5 + r0 * cos(t); y = r0 * sin(t); }
12 : //border Ci(t=0,2*pi) { x = 5 * cos(t); y = 5 * sin(t); }
13 : real current, currentC0, currentC1, currentC2;
14 : real V1, V2;
15 : mesh Th = buildmesh(C01(-140) + C02(-200) + C03(-140) + C04(-200)
16 : + C1(-20) + C2(-20));
17 : plot(Th, ps="four_probe_rect_mesh.eps", wait=true);
18 : fespace Vh(Th,P3);
19 : Vh uh,vh; // uh: potential
20 : problem Electro(uh,vh) =
21 : int2d(Th)(1.0 * ( dx(uh)*dx(vh) + dy(uh)*dy(vh) ))
22 : // + on(C0,uh=0)
23 : + on(C1,uh=1)
24 : + on(C2,uh=-1) ;
25 : Electro;
26 : plot(uh, ps="four_probe_rect_potential.eps", wait=true);
27 :
28 : //currentC0 = int1d(Th, C0) (N.x*dx(uh) + N.y*dy(uh)) ;
29 : currentC1 = int1d(Th, C1) (N.x*dx(uh) + N.y*dy(uh)) ;
30 : currentC2 = int1d(Th, C2) (N.x*dx(uh) + N.y*dy(uh)) ;
31 : V1 = uh(-0.5, 0);
32 : V2 = uh(0.5, 0);
33 : //currentC2 = int1d(Th, C2)(efh);
34 : cout << "currentC0 = " << currentC0 << endl;
35 : cout << "currentC1 = " << currentC1 << endl;
36 : cout << "currentC2 = " << currentC2 << endl;
37 : cout << endl;
38 : cout << "V1-2 = " << V1 - V2 << endl;
39 : cout << "F = " << currentC1 / (V1 - V2) << endl;
40 : sizestack + 1024 =1664 ( 640 )
-- mesh: Nb of Triangles = 110370, Nb of Vertices 55544
-- Solve :
min -1 max 1
currentC0 = 0
currentC1 = 1.73683
currentC2 = -1.73699
V1-2 = 0.41885
F = 4.14666
times: compile 0.009742s, execution 11.942s, mpirank:0
これによる結果 F = 4.147 は、JIS 規格で厚味を無視できるとした時の値
F = 4.235 より、2.1% 小さい値となっている。
ちなみに、上記のコード内の plot 文で表示される mesh と equi-potential curve は次のようになる。
まとめ
4 探針法を FEM でシミュレートするにあたり、- 導体中の電位分布は真空中のそれと同じ微分方程式で与えられる
- 電流プローブを小さい円形の境界 (C1, C2) で与え、 それに電圧を境界条件として与える (例えば ±1 V)
- サンプルの形状を表わす境界 C0 では電圧の境界条件は与えない
- FEM にてシミュレーションを実施、$u$ の分布を求める
- C1, C2 での法線方向の電流をその境界上の線積分で求める $(I_0)$
- 電圧プローブの位置での電位を $u(x, y)$ として読み取る (V1, V2)
- $F = I_0/(V1 - V2)$ によって、変換係数を求める
61/1,737,172